Table of Contents
In this post I continue our series of articles about portfolio management. I go on with further, a bit more detailed continuation of the theme. I further develop the issue of Compounding, I explain Discounting, Annualisation, Continous Compounding/Discounting. In the next posts we will move on from the basics to the definitions like Risk, portfolio theory, etc.
The first part os the Portfolio Management series explaining the basic definitions and concepts can be found here.
Every portfolio manager has a lot of issues to understand and oversee while looking after a portfolio of assets. It is absolutely necessary to try and understand as much as possible as to what drives the eventual performance and how to measure it. In the last post I finished with explaining Compounding in general. Now I’d like to continue studying this phenomenon. Let’s move ont o it…
Compounding further explained
Compounding Periods (CP) can in general be equal, longer or shorter than the Holding Period (HP) of an investment. Let’s now study all these cases one by one.
When CP = HP we can say that the following equation holds:
Future Value (FV) = Present Value (PV) x (1+ Interest Rate)
Here it is simply a 1-to1 relation. As the time we hold an asset equals the time of interest compounding, there’s just a simple time value of money relation here. One period of holding and one interest capitalisation. The term (1+Interest Rate) is the Capitalisation Factor (CF). It is the rate by which 1 CU (currency unit) of invested capital will grow invested at the given interest rate over one period of time.
Let’s take an example: John decided to invest $1000 of his spare money in a one-year bond yielding 5% coupon. He buys the bond at par ($100), hence the Yield to Maturiy (YTM) is also 5%. The issuer of the bond pays the interest at the redemption date of the bond. In this case we have CP=HP. John’s investment FV = $1000 x (1+0.05) = $1050.
But what if CP < HP?
Here things get a little bit more complicated. In the simpliest situation of 2 CP’s within one HP we have the following situation we have to deal with:
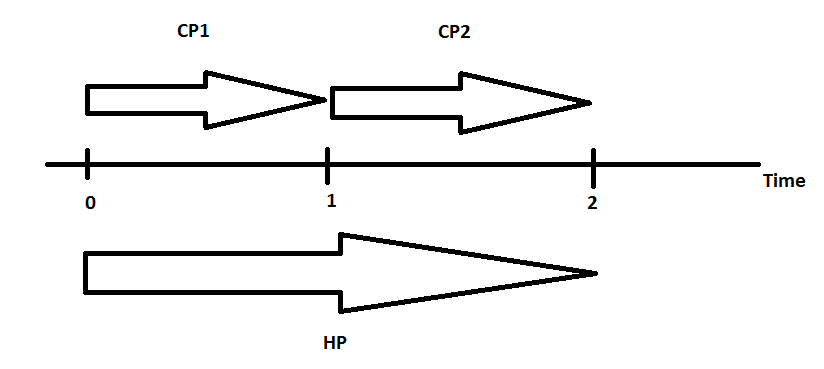
Interest is paid twice here: at the end of period (0,1) and at the end of period (1,2). Thing is that the interest paid at the end of period (0,1) can be reinvested as well and also earn interest (remember? compounding is interest on interest!). Here we have the following Capitalisation factor (CF):
(1+Interest(0,2)) = (1+Interest(0,1)) x (1+Interest(1,2))
As you can see in the second period it’s not only the capital that works out further interest, but also the interest from the first period earns additional interest. The longer then HP and the more CP’s the bigger the eventual “snowball effect” is. Meaning the bigger the total capital working out further interest.
Example: Lilly has $1000 of savings and decides to put it in a bank account for 3 years. The interest paid on the account is 3% p.a.. What amount will Lilly have after 3 years in her account? You have: HP = 3 years, number of CPs = 3 within 1 HP of 3 years. FV = $1000 x (1+0.03) x (1+0.03) x (1+0.03) = $1092.727. In a simple situation of just 1 CP within the 3-year HP the FV would be: FV = $1000 x (1+0.09) = $1009. The additional $2.727 Lilly gets over three years is the capitalisation effect (effect of interest on interest).
Now let’s study the 3rd situation, in which the CP > HP. We can present this situation as follows on the below graph:
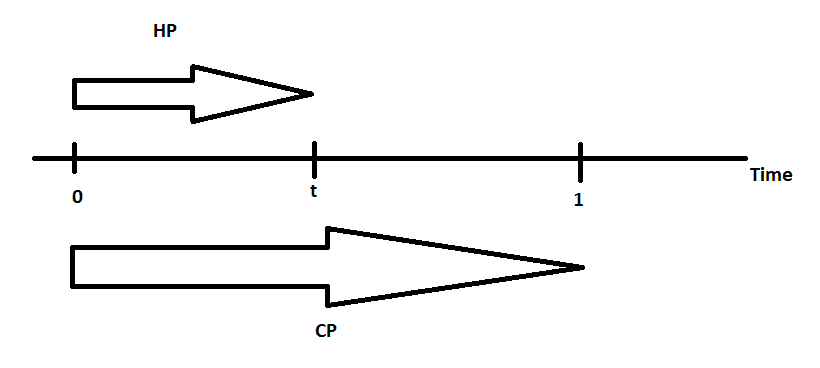
As you see here HP is a proportion of CP smaller than 1. Specifically we can name “t” the number of days for a HP. CP on the other hand can represent one full year (360 or 365 days depending on geography; we will use 360 for easier calculations). So the interest earned on every dollar (or the CF) in period (0,t) will be:
(1+Interest(0,t)) = (1+Interest(0,1))^t/360
Effectively we’re taking the full year interest to the power equal to the proportion of HP/CP (or t/360 specifically).
Example: Edward got $500 from his mother and needs to give it back to her in 6 months. Meanwhile he wants to invest this money. He goes for a bank deposit with his bank at 4% p.a. for the 6 month period. Here we have: HP=180, CP=360. What’s Ed’s profit? FV = $500 x (1+0.04)^180/360 = $509.9. Ed earns $9.9 in 6 months and gives the capital back to his mom ($500).
Continous Compounding
Let us say that EI is the Effective Interest Rate of Return. EI you can write as:
(1+EI) = (1+Interest(0,1)/m)^m
where “m” is the number of Compounding Periods (CP) within one Holding Period (HP).
The more CPs within one HP the more the Compunding Factor (CF) represented by (1+Interest(0,1)/m)^m leans towards the exponential of Interest(0,1). In an extreme case of close to infinite number of CPs in one HP we get :
(1+EI(0,1)) = e^Interest(0,1)
where “e” is the Euler number = 2.71828. This imples that for extremely small periods of time we get an interest “i” or continously compounded return:
i = ln(1+EI(0,1))
So, using the characteristics of logarythms and without going much further into maths here we can generally show that for very short periods of time a percentage change (or “i”) can be approximated by the difference between natural logarythms of the prices of an asset:
i = ln(Px1/Px0) = ln(Px1) – ln(Px0)
But this obviously does not hold for longer periods. Still because of it’s easy application people often use it for daily, hourly changes of assets. Continously compounded returns are additive, unlike normal returns.
Annualisation
To annualise means to present a certain holding period (HP) return as an annual rate of return. The financial industry uses it very often as it fits usual reporting and budgeting as well as taxation periods, which are most often one year. If you have a simple Holding Period Return (HPR), you can show it as an Annualised Return (AR):
(1+AR) = (1+HPR)^360/t
where “t” is the Holding Period (HP) in days.
You will find annualised rates of return in most of the reports describing the performance of different asset managers, investors, etc. It is important to understand that.
In the case of continously compounded returns annualisation takes the form of:
ia = 360/t x ln(Px1/Px0)
where “ia” is the annualised continously compounded rate of return.
Discounting
To make story short here: discounting is the opposite of compounding. You can write it as follows:
Present Value = Future Value / (1+Interest Rate)
What we call the Discount Factor (DF) is the 1/(1+Interest Rate) part fot he above equasion. This is true assumed the Interest Rate here corresponds to the Holding Period (HP). If the HP is longer than the Interest Rate period (say annual), we have to adjust it appropriately:
Present Value = Future Value / (1+Interest Rate)^n
Example: Amy knows that she will need $10 000 for her son’s education in 3 years time. She wants to know how much money she needs to put aside now to be able to afford that once the time comes. The interest rate at her bank is now 6% p.a. for a 3-year deposit. How much shall Amy put aside now? PV = $10 000/(1+0.06)^3 = $8 396.19. If she puts that amount on the deposit now, she will have exactly $10 grand in 3 years time.
In case of continous discounting the general rule will be (for one HP): PV = FV/ e^Interest(0,1).
Conclusions
We have covered just little part of the basics used in measuring, managing and understanding investing and portfolio management. There’s a lot more to learn of course, which by far stands out of scope of this series of articlels. There’s quite a bit of additional knowledge in the multiple books available for purchase, including the books I personally recommend. I wrote about them here in one of my eariler posts. There’s also a tremendous amount of learning courses for the ones willing to develop towards internationally renowned liceses like CFA, CAIA, CIIA, CFD, CIMA, etc. You can find some explained and described here or here. I for instance currently dig through the final level CIIA preperation materials by the Swiss Financial Analysis Association (SFAA). I find them extremely well prepared and high added-value. You can learn more about SFAA and its charter CIIA here.
Disclaimers: None of the ideas, views and thoughts presented here shall ever be taken as a recommendation to buy or sell stocks,bonds,FX,commodities or any other financial instruments as stated in REGULATION (EU) No 596/2014 OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL of 16 April 2014 on market abuse (market abuse regulation) and repealing Directive 2003/6/EC of the European Parliament and of the Council and Commission Directives 2003/124/EC, 2003/125/EC and 2004/72/EC or the Polish Act of 10 February 2017 amending the act on trading in financial instruments and some other acts. The article is for educational reasons and purely presents private views of the author, thus the author shall not be held accountable for any losses of a third party resulting from any potential trading activities in any instruments, both specifically or by category of assets. The author uses his best knowledge and data from sources believed to be reliable, but makes no representations as to the accuracy of the data.Full Disclaimers&Liability Limitations page.











