Table of Contents
Today we continue our journey through the tough matter of portfolio management. I describe and explain what is called risk on ex-ante (probabilistic) terms and describe some of its measures.
We have covered the Basics in the preceeding two posts here and here. Those of you who have not yet had a chance to go through them are invited to do so, as some of the ideas and issues here are a direct extention of the the basic ideas explained earlier. In xplaining the basics we worked on ex post terms. It means we measured what already happened before. But what is possibly the biggest added value of the modern portfolio theory is that is gives us tools to estimate returns on ex ante basis. In other words it allows us to measure both expected returns and the risk that comes with it. And here is where the concepts of probability step in for help.
Basic issues of probability
Let’s quickly explain the concepts helping understand the matter of probability:
👉 Sample (S) – a possible outcome.
👉 Sample Space (SS) – a set of possible outcomes.
👉 Probability (P) – a number we can associate with every Sample (Outcome).
👉 Probability Distribution Function (PDF) – a function in a P (Y axis) and Sample (X axis) space showing the P for every possible S.
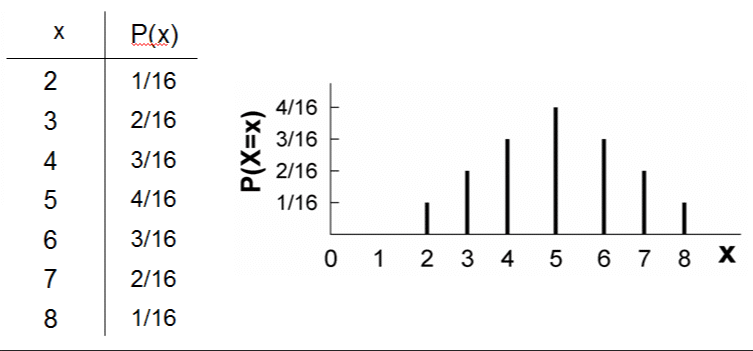
Example 1 of a PDF:
Probability presentation
There’s a few ways of presenting Probabilites (P). Two major ones are (a) Probability Trees (b) Probability Distributions.
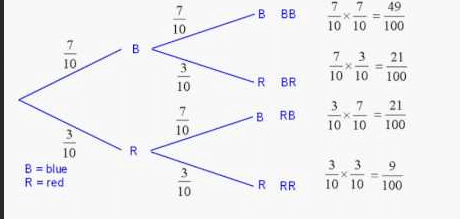
Probability Trees are a graphic form of presenting the probability of specific Outcomes (Samples). Mostly used are the so calles Binomial Trees. They only have two possible outcomes at every point in time. Here’s an example of how a binomial tree might look like for a 2-period time exercise for an exemplary stock (in each case stock has a 70% chance of going up and 30% chance of going down):
There are also multinomial trees (3 outcomes or more). The more possible outcomes the more dense the trees become.
Probability Distributions (PD) can be either (a) discrete or (b) continuous. Discrete PDs have a finite number of outcomes and are mostly presented in the form of histograms, as in Example 1. Discrete PDs can also be in the form of ranges, which is more useful for measuring financial assets returns. They can look like this for an exemplary portfolio of assets:
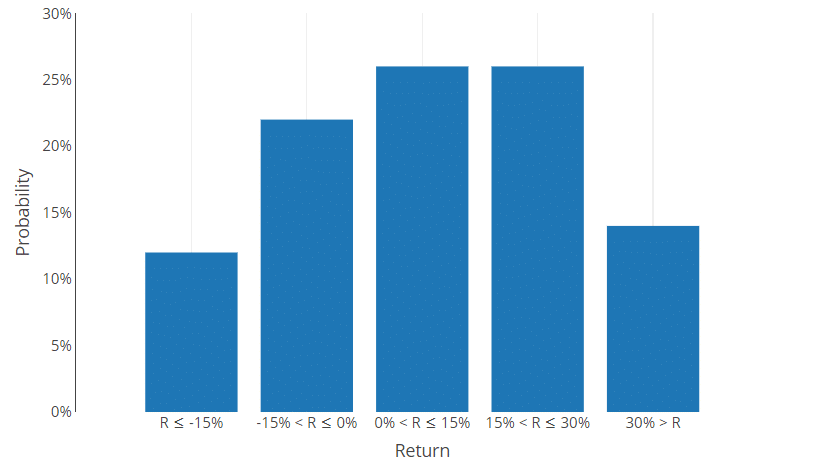
If we keep cutting the ranges of possible outcomes into smaller and smaller pieces, we will end up with a Continuous Probability Distribution (CPD). There’s different CPDs. More on this later. Here let’s just take a look at how a Normal CPD looks like:
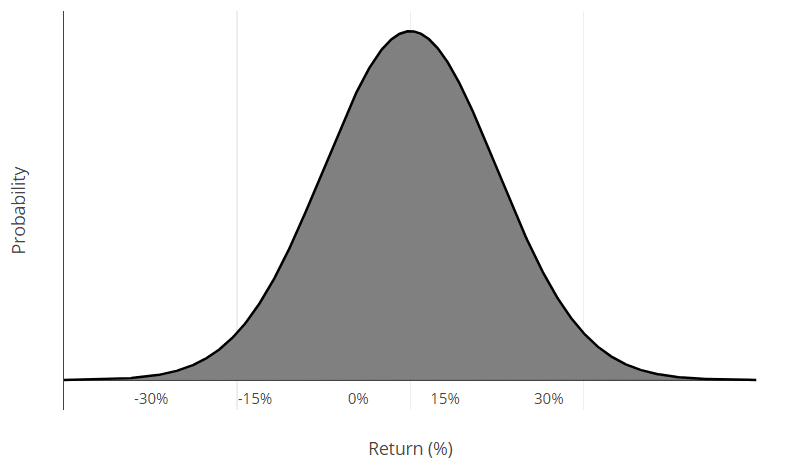
The whole area below the bell curve adds up to 100% probability of outcomes. It is called the the Probability Density Function (PDenF). It allows us to calculate and read the probabilities of returns below or above a certain treshold. The area below blowe the bell curve upto any given return (R) on axis x is the probability of possible outcomes (i.e. returns of a stock ora portfolio) not higher than R (name it P1). On the other hand the rest of the area depicts the outcomes higher than R (or P2 = 1-P1):
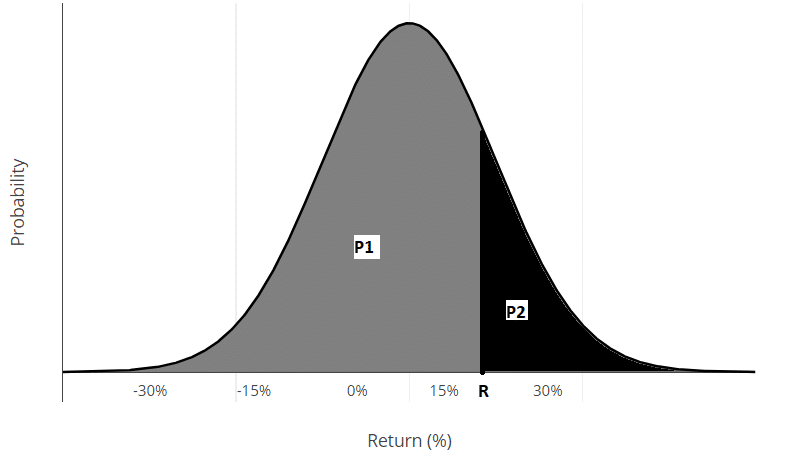
Measuring return distributions
Most practitiners use two major measures to describe distributions: (a) central tendency and (b) dispersion. With these two measures we’re able to tell a lot andmost of what is necessary about most distribution functions.
As far as the central tendency is concerned, there’s usually 3 measures used:
👉 Mean – the expected value of all outcomes;
👉 Median – the middle point of all outcomes or else the outcome of which 50% are higher and 50% are lower;
👉 Mode – the most frequently observed outcome.
Graphically the three above measures look very differently, dependant on whether we’re talking about a Symmetrical (Normal), Positively (Right) Skewed or Negatively (Left) Skewed Disribution. Here’s how it looks like:

Dispersion measurement
There’s several ways of dispersion measurement in a probability distribution:
👉 Set of possible outcomes – it’s just a list of all possible outcomes (values);
👉 Variance – measures squared deviations from the mean. Why squared? Because naturally deviation from the mean can be positive or negative. Hence, if you don’t get rid of the positive/negatie values by each observation, they will be netting out each other, blurring the real picture of a given distribution. The squaring solves this problem and gives each observation an absolute positive value. Unfortunately the Variance does not help that much in terms of interpreting the deviations, as it is expressed in different units than the Mean itself. To solve this problem the Variance is square-rooted again to get the…
👉 Standard Deviation – the square root of Variance. It tells us how spread-out a group of observations is from the mean. Measured in same units as the Mean. That’s why it is much more often used in finance and everyday life. The Modern Portfolio Theory uses SD is the main risk measure.
👉 Skewness – measures the assymetry of the distribution . Can be negative (left) or positive (right). Big skewness means long one-sided tail of outcomes. It’s the 2nd moment of distribution.
👉 Kurtosis – the 3rd moment of distribution. It measures extreme values in either tail (unlike Skewness). Higher Kurtosis means more extreme outcomes, smaller Kurtosis means less extreme outcomes. This moment can be mesokurtic (similar to normal distribution), leptokurtic (positive Kurtosis, implies most of observations in a narrow range but also a reasonable amount of extreme outliers, also called “skinny”), platykurtic (negative Kurtosis, this one is less concentrated around the mean, but also has less extreme outliers, is kind of flatter). Kurtosis for a normal distribution is 3.
Normal distribution
Normal distribution is the most commonly used one in the space of finance. That’s why, before we move on, I think it’s worth looking into it in more details.
Normal distribution is bell-shaped, is ideally symmetrical (Mean=Media=Mode) and has the following distibution characteristics in terms of standard deviation:
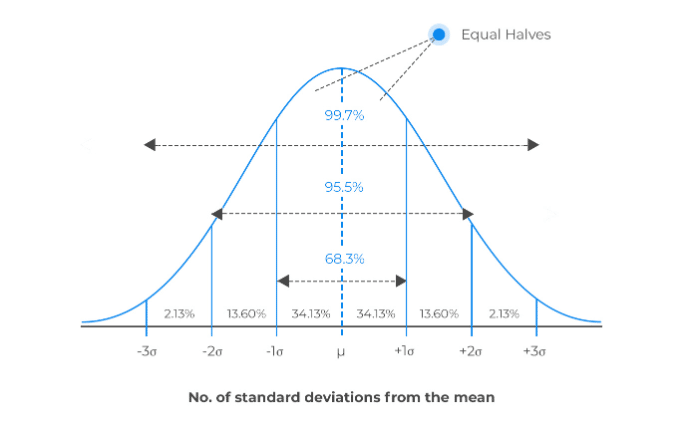
To summarize the above graph:
👉 68.3% of the outcomes in a normal distribution fall within 1 standard deviation (SD) from the mean;
👉 95.5% of the outcomes in a normal distribution fall within 2 SD from the mean;
👉 99.7% of the outcomes in a normal distribution fall within 3 SD from the mean.
Every normal distribution has a different Mean and SD of course. This makes probability calculations tougher. But there’s the process of standardization that comes with help here. Namely, you can transfrom each normal distribution into a standard normal distribution with a Mean=0 and SD=1. This process is being done by subtracting the Mean from the variable (i.e. return) and dividing it by the SD. Such distribution is easy to interpret. There are special statistical tables allowing you to easily read the probability of a specific outcome (lower than treshold Z) without doing many difficult calculations. They look like this:
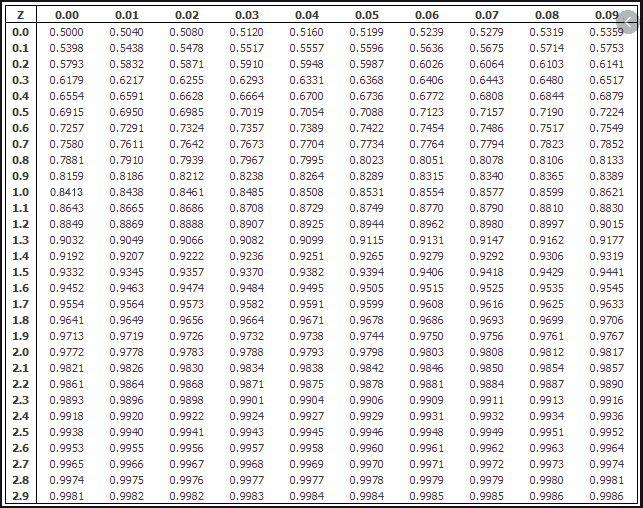
Covariance
There is one other concept that is crutial in using statisticls in finance (and portfolio theory specifically). It’s the Covariance. Covariance is nothing else, but the degree at which two variables (i.e. two different stocks) move in the same direction. You say that two stocks covary. Again, similarly as in case of Variance and SD, Covariance is not a standardized measure. To put the covariance into easy-to-interpret framework the Correlation Coefficient (CC) is used. It is obtained by dividing the Covariance of two variables (i.e. two stocks) by the product of each of the variables (stocks) SD:
CC = Cov (A,B)/SD(A)xSD(B)
CC is always within the range [-1,1]. A CC of -1 means perfect negative correlation (stock A goes up 1%, stock B goes down by 1%). CC of 1 means perfect positive correlation (stock A goes up 1%, stock B goes up by 1%). CC of 0 mean no correlation between A and B at all (stocks move randomly against each other with no specific trend).
Uffffff….enough for today 🙂
In the next post we will start the insights of Portfolio Theory.
Best,
GlobalAlphaSearch.com
Disclaimers: None of the ideas, views and thoughts presented here shall ever be taken as a recommendation to buy or sell stocks,bonds,FX,commodities or any other financial instruments as stated in REGULATION (EU) No 596/2014 OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL of 16 April 2014 on market abuse (market abuse regulation) and repealing Directive 2003/6/EC of the European Parliament and of the Council and Commission Directives 2003/124/EC, 2003/125/EC and 2004/72/EC or the Polish Act of 10 February 2017 amending the act on trading in financial instruments and some other acts. The article is for educational reasons and purely presents private views of the author, thus the author shall not be held accountable for any losses of a third party resulting from any potential trading activities in any instruments, both specifically or by category of assets. The author uses his best knowledge and data from sources believed to be reliable, but makes no representations as to the accuracy of the data.Full Disclaimers&Liability Limitations page.